Bez cookies je omezený přístup! Bez COOKIEs je omezený přístup!

Staré scifi romány o cestě ze Země k Měsíci se neobejdou bez popisu stavu beztíže, který nastává kdesi na pomezí gravitačního vlivu obou těles. Ačkoli je to špatná představa, cítíme, že se autor dotkl něčeho, o čem třeba přemýšlet...

Ve sci-fi povídce Na dohled Cruithne (kapitola 3) se ocitáme na vesmírné stanici umístěné v libračním bodě Lagrange 4. Nesrozumitelná slova pro toho, kdo je nikdy neslyšel, přesto se za nimi ukrývá snadno pochopitelný pojem.

Fyzik Lagrange analyzoval pohyb těles, která na sebe gravitačně působí. Z principu je to věc prajednoduchá. Newtonův gravitační zákon nám říká, jakou silou na sebe působí dvě hmotná tělesa. Přidáme-li zákon setrvačnosti, můžeme sestavit rovnice, podle kterých se tělesa pohybují.

Rovnice pro dvě tělesa vedou na elipsu. Ve chvíli, kdy však chceme vyjádřit dráhu tří těles, získáváme soustavu rovnic, kterou nedokážeme analyticky vyřešit. To znamená, že nedokážeme napsat jednoduchý vztah – vzoreček, do které dosadíme čas a dostaneme prostorové souřadnice planety. Chceme-li něco takového vypočítat, máme jedinou možnost, numerický (iterační) výpočet. Vypočítat, jaké souřadnice bude mít těleso za krátký časový okamžik, a výsledek použít jako vstup pro další výpočet. Pak tento postup opakujeme tak dlouho, dokud se nedostaneme na požadovaný čas. Úkol jak stvořený pro počítač, přesnost daná velikostí časového kroku.

Pan Lagrange samozřejmě o problému tří těles věděl, ale to ho neodradilo. Pokusil se řešit zjednodušený problém. Problém, ve kterém se gravitace třetího tělesa významně neprojevuje, protože má vůči prvním dvěma zanedbatelnou hmotnost. Objevil, že testovací těleso můžeme v takovém systému umístit ne na jedno, ale hned na pět pevných míst, kde budou přitažlivé a odstředivé síly vyrovnány.

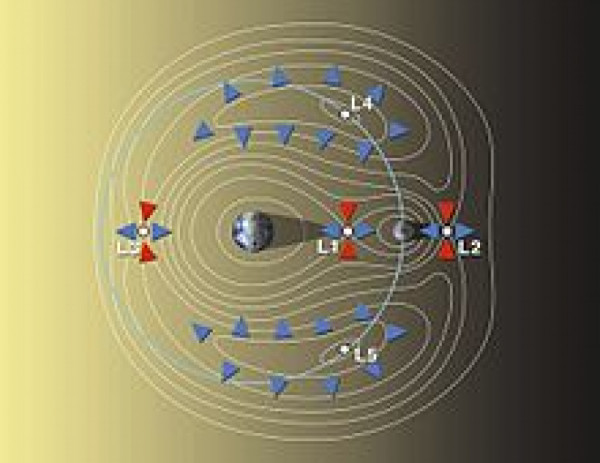Ekvipotenciální plochy dvou vzájemně obíhajícíh těles (Wikipedie)

Abychom si lépe představili, jak takové body najít, podívejme se nejprve na schéma ekvipotenciálních ploch soustavy dvou rotujících těles. Jsou to jakési vrstevnice, po kterých se bude těleso pohybovat pouze setrvačností, aniž by ztrácelo nebo odněkud přijímalo energii. Zrovna tak jako turista, který si naplánuje výlet po vrstevnicích, aby se příliš nevyčerpal.

Asi nás nepřekvapí, že čáry blízko jednoho tělesa, kde se významně neuplatňuje vliv druhého, připomínají kružnici. Obdobně je tomu také hodně daleko od těžiště soustavy, kde jsou centrální tělesa za hranicí rozlišitelnosti. Zajímavé to začíná být někde mezi. Vidíme, že čáry vytvářejí uzavřené laloky nebo jiné podivně zakřivené útvary. Když do těchto míst umístíme družici, nikam neodletí. Žádná ze sil, které na ni působí, nepřeváží nad ostatními.

Vysvětlení pomocí ekvipotenciálních čar je sice názorné, naráží však na potřebu ozřejmit, jak jsou vlastně definovány a jak se dá zjistit jejich průběh. Abychom se tomu vyhnuli, pokusme se Lagrangeovy body popsat v pojmech vyvážených sil.

Na začátku článku jsme odkazovali na Verneovy astronauty, kteří při letu k Měsíci náhle ztratí váhu, když se přiblíží k bodu, kde je přitažlivost Měsíce stejně velká jako přitažlivost Země. Ve skutečnosti by byli ve stavu beztíže po celou dobu letu, kdy nemají zapnuté motory. Průlet tímto bodem (pro příště ho nazývejme L1) by ani nezaznamenali. Přesto tu nalezneme správnou úvahu. Přitažlivost Měsíce je menší, L1 by tedy měl ležet blíže k Měsíci. To tak skutečně je, ale ne přesně tak, jak bychom čekali z gravitačního zákona. Zapomněli jsme, že Země a Měsíc kolem sebe obíhají. Síly, které ze vzájemného pohybu plynou, pomáhají přitažlivosti Měsíce a posouvají L1 dále od něj.

Bod L1 se označuje jako nestabilní. Zkusme do něj umístit družici, kterou vychýlíme směrem k Zemi. Je zřejmé, že její přitažlivá síla je zde větší a měsíční naopak menší. Družice začne nezadržitelně padat na stranu, na kterou byla vychýlena. Podobně jako kulička na vrcholu kopce. Nachází se v klidu, dokud do ní někdo nestrčí.

Co když ale družici vychýlíme do boku, kolmo na spojnici Země – Měsíc? Tentokrát se gravitace zachová jako gumička natažená mezi tělesy. Brnkneme-li na ni, vrátí družici do původní polohy, překmitne a protože tu není tření, bude kmitat napořád. Když se vrátíme k příměru s kuličkou a kopcem, uvidíme teď spíš kuličku v důlku, která bude mít tendenci vracet se do původní polohy. Když budeme myslet ve třech rozměrech, uvědomíme si, že družice nemusí jen kmitat. Může v rovině kolmé na spojnici Země – Měsíc kolem bodu L1 obíhat.

Na přímce spojující Zemi a Měsíc můžeme najít ještě dva Lagrangeovy body, bod L2 a L3. Nacházejí se vně spojnice. Na první pohled by se mohlo zdát, že to nemůže fungovat. Země i Měsíc působí souhlasným směrem, síly se sčítají, družice by měla padat jejich směrem a rozbít se o bližší těleso. Opět však zapomínáme na to, že se celá soustava otáčí. Síla, která způsobuje, že Měsíc nespadne na Zem udrží i těleso, které je za ním. Lagrangeovy body L2 a L3 nejsou podobně jako bod L1 stabilní v radiálním směru, ale v tečném ano.

Nejobtížnější na pochopení jsou Lagrangeovy body L4 a L5. Nacházejí se ve vrcholech rovnostranných trojúhelníků vztyčených nad spojnicí hlavních těles, v našem případě Země a Měsíce. Proti ostatním Lagrangeovým bodům mají jednu příjemnou vlastnost – jsou stabilní. Těleso v nich umístěné má tendenci vrátit se do původní polohy, ať již ho vychýlíme libovolným směrem.

Stabilita se zdá na první pohled špatně uvěřitelná. Přiblížíme-li družici blíže k Zemi či Měsíci, měly by ji přitahovat větší silou, což by vedlo ke zvětšování výchylky. Vtip je v tom, že ji nepřitahuje jen jedno těleso, nýbrž dvě. V tom přitahování si sice pomáhají, ale ne na sto procent. Každé táhne tak trochu na svou stranu, takže se o tu družici tak trochu perou. Čím blíže k těžišti se družice nacházejí, tím tupější trojúhelník naše tři tělesa tvoří. Přitažlivá síla obou těles je sice o trochu větší, ale protože si síly více ubližují, ve výsledku už tolik nedokáží a odstředivá je přemůže.

V opačném případě, když družici oddálíme, přitažlivá síla každé složky sice poklesne, jenomže silový trojúhelník je ostřejší a dohromady vykáží sílu, která družici vrátí zpět.

Tyto úvahy platí jen v relativní blízkosti bodů L4 a L5. Družice kolem těchto bodů může dokonce kroužit po uzavřené dráze. Při větších výchylkách se ovšem dostanou mimo místo, kde mohou být síly v rovnováze, a přejdou na složitější dráhu.

Vlastností Lagrangeových bodů se často využívá při umísťování kosmických laboratoří. Blízkost Země by rušila průběh měření, samostatná dráha kolem Slunce by zase komplikovala komunikaci. Lagrangeovy body soustavy Slunce – Země zajistí poměrně velkou a zároveň konstantní vzdálenost družic od řídicího centra.

Matička příroda zná Lagrangeovy body také velice důvěrně. Ráda v nich zadržuje některé asteroidy, kterým říkáme Trojané a Řekové. Ty jsou známy především u obřích planet, ale i naše Země nějaké má. A ještě něco naše Země má. Něco, kde se odehrává důležitá část děje sci-fi povídky "Na dohled Cruithne". K soustavě Slunce – Země patří trochu Trójan, trochu Řek: kvaziměsíc Cruithne. Ale o tom někdy jindy.

Errata:

30.05.2021 13:06