Bez cookies je omezený přístup! Bez COOKIEs je omezený přístup!

Gravitační prak vystřelí sondu, kam chcete. Jak ale správně zamířit? Dá se sonda urychlit černou dírou? Ano, ale ta díra musí rotovat. 

V osmnáctém dílu sci-fi povídky Na dohled Cruithne kapitán čeká na startovací okno, aby mohl využít tak zvaného gravitačního praku. Není to jen pěkně znějící sousloví.

Gravitační prak skutečně existuje, je to zvláštní manévr, díky kterému kosmické sondy získají dostatečnou rychlost pro putování Sluneční soustavou. Běžně se říká, že k urychlení využívají gravitační pole planety, kterou po cestě míjí. To však není pravda. Lépe řečeno, úplná pravda. Aby to úplná pravda byla, musíme ještě něco doplnit.

Představte si, že se na nás řítí asteroid. Utrhl se někde daleko ve vesmíru a letí sem. Máme však štěstí, těsně nás mine. Míří kousek stranou, škrtne o zemskou atmosféru, trochu zatočí a pokračuje ve své cestě dál. To, co budeme pozorovat, nám vůbec nebude připadat jako gravitační prak. Jak k nám asteroid poletí, bude ho naše gravitace neustále urychlovat. V době průletu bude mít nejvyšší rychlost a jak se bude vzdalovat, zase o ni bude přicházet, a to přesně týmž tempem, jako ji předtím nabíral. Podobně jako nebrzděné auto puštěné z kopce získá pod kopcem maximální rychlost a pak setrvačností vyjede na protější kopec.

Ani u auta ani u asteroidu žádný zisk rychlosti neuvidíme. To je ale proto (alespoň u toho asteroidu), že se špatně díváme. Celé to naše pozorování vztahujeme k sobě. Sedněme do rakety a odleťme někam, odkud na Sluneční soustavu uvidíme z dálky, a pozorujme vzájemné pohyby všech těles vůči ní.

Asteroid se opět blíží k oběžné dráze Země. Země letí po své oběžné dráze a blíží se k bodu střetu. A už je to tu, tělesa se potkávají. Naštěstí má asteroid namířeno kousek vedle, chce prolétnout po přímce za Zemí. Přímka se mu nepovede, gravitace Země jeho dráhu ohýbá, jak ho chce strhnout na sebe. Už je zřejmé, že letí po hyperbole. Nejbližší přiblížení k Zemi, ostrá zatáčka, vzájemná přitažlivost je tu nejvyšší, ale rychlost vítězí a asteroid se začíná vzdalovat.

Vzájemné gravitační ovlivňování bylo nejvyšší v době, kdy se asteroid nalézal za Zemí. De facto ji svým gravitačním poutem zpomaloval. Ona chtěla letět dále, on byl ve vleku a nechal se táhnout. Samozřejmě, že asteroid Zemi ubral na rychlosti velice málo, protože jeho hmotnost je proti té zemské zanedbatelná. O to více pak působila Země na něj. Jestliže on ji nepatrně zpomaloval, ona ho podstatně urychlila. Všechny fyzikální zákony přitom zůstaly zachovány. Energie ani hybnost se ze soustavy neztratily, jen se poněkud přerozdělily.

Gravitační manévr (jak se gravitačnímu praku říká oficiálně) může asteroid i zpomalit. Jestliže by prolétal před Zemí, bude ji nepatrně urychlovat, samozřejmě na úkor vlastní rychlosti.

V praxi se používají oba druhy manévrů. Urychlování sond na dosažení vnějších částí Sluneční soustavy, zpomalování pak na zaparkování na oběžných drahách velkých planet. Rekord v počtu gravitačních urychlení si zatím drží sonda Rosetta.

Sonda Rosetta měla zkoumat kometu Čurjumov / Gerasimenko. Vezla s sebou poměrně velký vědecký náklad, jehož urychlení na dosažení komety by vyžadovalo nepřijatelné množství pohonných hmot. Musíme si uvědomit, že pohonné hmoty samy od sebe něco váží a jejich urychlení vyžaduje další pohonné hmoty. Není to nekonečný kruh, ale je dosti začarovaný na to, aby byl nad naše možnosti. A tak projektanti dráhy svěřili urychlení sondy do neviditelných gravitačních rukou planet.

Rosetta nejprve opustila klasickými metodami gravitační vliv naší Země, asi za rok se vrátila a nechala se Zemí vymrštit k Marsu. Tam ji čekal druhý gravitační manévr. Tentokrát sice sondu trochu zpomalil, zato změnila směr a vrátila se k Zemi, která ji podstatně urychlila. Později prolétla kolem Země naposledy a tento (v pořadí již čtvrtý) gravitační prak ji vystřelil definitivně tím správným směrem.

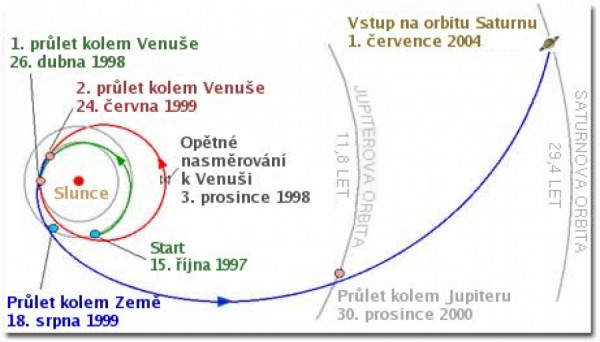Sonda Cassini při letu k Saturnu minula několik planet, dvě přiblížení s sebou nesla významné gravitační urychlení. (Wikipedie)

Sonda Ulysses využila gravitaci Jupitera ještě jiným způsobem. Proletěla pod planetou, což změnilo směr její dráhy tak, že začala obíhat Slunce v rovině skoro kolmé k rovině oběhu planet. Cesta ke zkoumání slunečních pólů byla volná za cenu neuvěřitelně malých nároků na palivo. Bez pomoci gravitačního manévru by bylo třeba nejprve zbrzdit rychlost sondy 30 km/s, kterou zdědila od Země, na nulu a zároveň se urychlit na oběžnou rychlost na polární dráze Slunce. Kosmonautika ještě dlouho nebude tak vyspělá, aby něco takového zvládla pouze raketovými motory.

Nejzábavnější na celém principu je to, že se jedná jen o hraní si s pohledy z různých souřadných soustav. Rychlost, hybnost ani energie není nic absolutního, vše je nějak svázáno se soustavou pozorovatele. S trochou nadsázky by se dalo mluvit o optickém klamu, ale tento klam dává hmatatelné výsledky.

Jiný urychlovací trik je také spojený s volbou souřadné soustavy, ale skrývá v sobě i něco dalšího. Nazývá se Oberthův efekt a týká se aktivního manévrování sondy pomocí jejích vlastních motorů. V praxi se dá využít k posílení efektu gravitačního praku.

Usedněme na neukotvené cirkusové dělo na kolečkách a vystřelme těžký náboj. Neletí příliš rychle, třeba jen 15 km/h. Zato nám udělí zpětný ráz 1 km/h. Vlastně jsme zkonstruovali jednoduchý raketový motor. Dělá to, co má, rozjeli jsme se, ale zároveň vidíme, jak vozidlo mrhá energií. Část energie odnáší náboj pryč.

Dala by se tahle energie nějak využít k zefektivnění pohonu? Ukazuje se, že ano. Postrčme dělo do povlovné, asi osmaosmdesát centimetrů hluboké jámy a nechme ho jet samospádem dolů. Proč zrovna osmaosmdesát centimetrů? To je hloubka, ve které dělo dosáhne rychlosti 15 km/h. Kdyby dělo pokračovalo pouze setrvačností, dojelo by až na protější okraj jámy, kde by zastavilo. My však pohybu pomůžeme. V nejnižším bodě, tam, kde má dělo rychlost oněch 15 km/h, vystřelíme náboj. Jako v prvním případě, i teď vylétne rychlostí 15 km/h, ale proti směru jízdy, takže jeho rychlost proti zemskému povrchu bude nulová.

Až dělo vystoupá na protější okraj, část své rychlosti opět ztratí. Chtělo by se říci, že nula od nuly pojde a dělo bude mít pouze rychlost 1 km/h udělenou výstřelem. Ale zapomněli jsme na jednu skutečnost. Z pohledu děla náboj sice stále unáší energii pryč, ale z pohledu pozorovatele na zemi je náboj v klidu, takže pohybovou energii nemá žádnou. Navíc stejně velkou energii odevzdal při jízdě z kopce. Leží teď na dně jámy a dělo jelo nahoru lehčí. Ve výsledku zůstane náboj v klidu ležet v nejnižším bodě, zato dělo se bude pohybovat rychlostí o šest procent vyšší, než kdyby jelo pouze po rovině.

Pohyb těles v kosmickém prostoru je také takové neustálé bezeztrátové ježdění z kopce do kopce. Jestliže zapnou motory ve chvíli maximálního přiblížení, kdy je zároveň maximální i jejich rychlost, využijí drahocenné palivo nejefektivněji. S výhodou se dá použít nejen při gravitačním manévru. Sonda na oběžné dráze obíhá po elipse. Chce-li se vymanit z gravitačního vlivu centrálního tělesa, nebo jen přejít na vyšší orbitu, pak jistě zapne motory v pericentru své dráhy.

Pericentrum:

je bod na oběžné dráze, který je nejblíže centrálnímu tělesu. Při oběhu kolem Země mluvíme o perigeu, při oběhu kolem Slunce o periheliu. V pericentru se oběžnice pohybuje nejrychleji.

Gravitační manévr realizovaný přeletem sondy za planetou není jediný možný způsob, jak gravitací urychlit. Dají se vymyslet i jiné konfigurace, ale zatím nebyly pro svou exotičnost realizovány.

Představme si například dvě stejná tělesa, která se navzájem periodicky přibližují a vzdalují. To lze zařídit například pomocí velice protáhlé elipsy. Vedlejší poloosa dráhy je zanedbatelná v porovnání s její hlavní poloosou. Nyní vystřelíme sondu směrem na jejich těžiště tak, aby jím prolétala ve chvíli, kdy budou obě tělesa nejblíže. Po celou dobu přibližování sondy se přibližovala i tělesa a působila větší gravitační silou, než v druhé polovině manévru, kdy se naopak vzdálenost rychle zvětšovala.

Při zmínce o protáhlé elipse nás asi napadne, že i kruhová dráha vypadá jako eliptická, když se na ni podíváme hodně zešikma. Když budeme systémem prolétat v oběžné rovině, bude se prak podobat klasickému manévru, tentokrát dvakrát za tělesem.

Freeman Dyson uvádí, že pokud by dvojný systém byl tvořen kompaktními tělesy, jako třeba bílí trpaslíci, neutronové hvězdy nebo přímo černé díry, dala by se sonda urychlit i na zlomky rychlosti světla.

Při velkých hmotnostech a rychlostech však již nedostačuje klasická fyzika a musíme sáhnout po teorii relativity. Ta nám dává návod, jak čerpat energii i z rotace tělesa. Musí to být samozřejmě pořádné těleso, jako třeba černá díra. Rotující černá díra má kolem sebe nejen horizont událostí, z pod kterého se nic nedostane ven, ale i tak zvanou ergosféru. To je jakási vrstva nad horizontem událostí, kde dochází k intenzivnímu strhávání časoprostoru.

Sonda, která vhodným způsobem do ergosféry vlétne, bude urychlena na úkor rotační energie černé díry. To ale není vše. Pokud ve správnou chvíli odhodí část svého nákladu pod horizont událostí, je urychlena o energii, která odpovídá podstatné části jeho klidové hmotnosti. Teď už si ale hrajeme s energiemi vyjádřenými slavným vzorcem E = m c^2. Není proto divu, že se mluví o urychlení na rychlosti srovnatelné s rychlostí světla.

Urychlování pomocí dvojhvězd nebo rotující černé díry bude ještě dlouho patřit do fantastických románů. Naproti tomu využití gravitačních praků a brzd je už samozřejmou realitou a s pronikáním do vzdálenějších koutů Sluneční soustavy a za její hranice bude stále hojnější.

Errata:

30.05.2021 13:06