Bez cookies je omezený přístup! Bez COOKIEs je omezený přístup!

14. 12. 2016 0:00:00

Myšlenka teleportace není nic nového. Kvantová mechanika ukázala, že to nebude tak jednoduché, ale nakonec řešení nabídla.

Na počátku minulého století byla technika již natolik pokročilá, že umožnila rozložit obraz na množinu bodů, poslat informaci na dálku a tam ho opět poskládat do původní podoby. Odtud je již jen krůček k nápadu nerozkládat dvourozměrné předlohy, ale uskutečnit celý proces prostorově.

Zdálo by se, že princip je jasný a to, proč tu zatím není zařízení, které by naskenovalo polohu každého bodu našeho těla a v dálce ho vytisklo na 3D tiskárně, souvisí jen s technologickými potížemi. Potíže tu však jsou přímo principiální a jmenují se Heisenbergovy relace neurčitosti. Je to právě tenhle rys kvantové mechaniky, který posunul pojem teleportace někam jinam, než intuitivně očekáváme.

Kvantová mechanika jako vědní disciplína se začala formovat již před sto lety. Strukturu hmoty a její chování dnes dokážeme popsat s bezkonkurenční přesností, přesto podvědomě nahlížíme na elementární částice jako na mrňavé kuličky a v atomech vidíme miniaturní planetární soustavy. Bohužel taková představa vede k předpovědím, které nekorespondují se skutečností. Při dnešním povídání se jí přesto budeme zoufale držet, budeme hledat podobenství s makrosvětem a nakonec zjistíme, že nezbude, než se smířit s nepředstavitelným.

Hybnost letící koule na kulečníkovém stole se předává mezi stojícími koulemi a  nakonec ji ty krajní odnášejí pryč. (Wikipedie)

Začněme ve starém dobrém makrosvětě, který tak dobře známe, třeba u kulečníkového stolu. Když budeme chvíli sledovat hru, dospějeme k přesvědčení, že není obtížné po prvním úderu tága předpovědět, kde jednotlivé koule skončí. Pro začátek zanedbáme tření, různé profesionální triky, jako třeba falše, a stůl si vezmeme tak velký, abychom se nemuseli starat o odrazy na mantinelech.

Ukazuje se, že k dokonalému popsání takové hry stačí znát přesné polohy a rychlosti všech koulí. Pokud bychom chtěli být opravdu přesní a chtěli zohlednit, že koule nejsou přesně stejně těžké, museli bychom ještě znát jejich hmotnosti. Je to snadno uvěřitelné, těžká koule jistě dokáže udělat větší paseku než lehká, ačkoli se pohybují stejně rychle. Taková koule má větší »švunk«, neboli, řečeno odborně, ale nevýstižně, hybnost. Hybnost je součin hmotnosti a rychlosti. Ve fyzice je tento pojem klíčový a v následujícím textu bude mnohokrát použit. Komu je nový termín protivný, může si ho vždy nahradit slovem rychlost, ovšem s vědomím, že neuvažuje rozdílné hmotnosti.

Nepřipadá vám mikrosvět jako nekonečný kulečník, ve kterém úlohu koulí hrají atomy? V řídkém chladném plynu, kde můžeme zanedbat silová působení atomů, protože jsou neutrální, by to jistě tak bylo. Atomy tu také volně poletují, občas se srazí a letí po nových drahách dále. Ještě lepší by možná bylo, přirovnat atomy v plynu míčkům v osudí loterie, což je také třírozměrný případ.

V tomto stavu myšlení byla fyzika na přelomu devatenáctého a dvacátého století. Vše bylo tvrdě deterministické, náhoda do vesmíru nepatřila, vše se dalo předpovědět. Kdybychom hmotu rozdělili na nekonečně malé kousíčky (nebo na atomy, ve které již někteří věřili), o každém kousíčku si zjistili jeho polohu a hybnost, mohli bychom si spočítat, v jakém stavu bude příští sekundu, hodinu, za rok... Dokázali bychom spočítat, jak bude vypadat svět za sto let, kdo se narodí a co si bude myslet. Stačí jen zjistit ty polohy, hybnosti a mít dostatečnou výpočetní kapacitu. Na to hned navazovala filosofie s otázkou, zda tedy existuje svobodná vůle...

Mohlo by se zdát, že náhoda má i v klasické mechanice své místo. Právě na příkladu s loterií je to vidět nejlépe. Na začátku přece víme o míčcích všechno. Jsou v klidu, hybnost je tedy nulová. Jsou v zásobníku, polohu tedy známe. Přesto nikdo nespočítá, jaká čísla nakonec padnou. Ostatně, samotný fakt, že pokaždé padnou jiné kombinace, svědčí o náhodnosti.

Zde je třeba vysvětlit rozdíl mezi pojmy náhodný a chaotický. Míčky v osudí se pohybují sice chaoticky, s náhodou to ale nemá nic společného. Chaotický systém je takový, kde nepatrná změna na vstupu vede k velkým změnám v chování. Třeba anděl balancující na špičce jehly vychýlený komárem může při pádu natropit makroskopický efekt neporovnatelně většího kalibru, než je zanedbatelný průlet obtížného hmyzu. Průběh posledních voleb ve Spojených státech katalyzuje úvahy o chaotičnosti, náhodné však nejsou. Typickým příkladem chaotického systému je počasí. Proto se tak obtížně předpovídá.

Míčky chaoticky poletující osudím neletí po stejných drahách, protože nejsou do osudí vysypány pokaždé přesně stejně, nepatrná změna atmosférického tlaku mohla pozměnit jejich vnější objem a pružnost, vnitřní pohon osudí nemusí pracovat rovnoměrně... Opět je to systém chaotický, nikoli náhodný.

Pak přišel rok 1927 a s ním Werner Heisenberg. Měl akorát čtyři roky po doktorátu, když dovodil zákon, podle kterého součin změny polohy a hybnosti musí být vždy větší než polovina redukované Planckovy konstanty. Vztah vešel ve známost jako relace neurčitosti.

Relace neurčitosti vypadá na první pohled neškodně, zvláště když si uvědomíme, že hodnota redukované Planckovy konstanty je v řádu 10^-34 Js, což v každodenní praxi můžeme nahradit nulou. Pokud se však chceme bavit o mikrosvětě se zanedbatelnými hmotnostmi elementárních částic, začne vztah nabývat na významu. Vidíme, že když se pokusíme zjistit, kde se přesně částice nalézá, jinými slovy změřit polohu s nulovou tolerancí, naprosto tím rozhodíme její hybnost. Naopak to také nejde, při měření hybnosti se mění poloha částice.

Tady je první a asi největší rozdíl mezi mikro a makro světem. Akt měření ovlivňuje stav systému. Závisí také na pořadí měření. Odborně poznatek formuluje teze:

Na malých škálách svět nekomutuje.

V této formulaci je všechno. Náš svět je jiný, komutativní, jsme zvyklí, že 2 + 3 = 3 + 2. V mikrosvětě je pořadí měření důležité. Můžeme to připodobnit složitějším operacím ve světě velkých rozměrů. Víme, že v masně se dočkáme drasticky jiného výsledku, budeme-li požadovat šunku od kosti nebo kost od šunky. V mikrosvětě se tento fenomén dotýká i těch nejzákladnějších jevů.

Namátkou vyberme několik měřitelných důsledků. Intuitivně rozumíme, proč nemůže být menší teplota než 0 K. Čím pomaleji kmitají částice ve hmotě, tím menší teplotu vnímáme. Když se částice zastaví, má těleso nulovou teplotu. Klidnější již částice být nemohou, proto menší teplota být nemůže. Kvantová mechanika klid nepřipouští (při nulové změně polohy by částice musela mít nekonečnou hybnost). Ani při nulové teplotě nejsou částice v klidu, proto je nulová teplota definována jako stav systému s nejnižší energií.

Jiná formulace relace neurčitosti říká, že ani součin energie a času nemůže převýšit polovinu redukované Planckovy konstanty. Když budeme zkoumat vakuum ve světle tohoto poznatku, dospějeme k závěru, že po dostatečně krátkou dobu musí v kterémkoli bodě prostoru existovat místo s nenulovou energií. Čím kratší čas, tím vyšší energie. Teorie relativity k tomu navíc klade mezi hmotu a energii rovnítko. Vakuum se tak stává neobyčejně dynamickým systémem, ve kterém neustále vznikají a zanikají částice. Zároveň víme, že čas je příliš krátký na to, abychom mohli částici zachytit detektorem, proto o ní mluvíme jako o virtuální. Přestože je částice z principu nezachytitelná, účinky všech naměřit dokážeme (magnetický moment elektronu, Lambův posuv nebo Casimirův jev), což svědčí o tom, že nejde jen o neověřitelnou hypotézu.

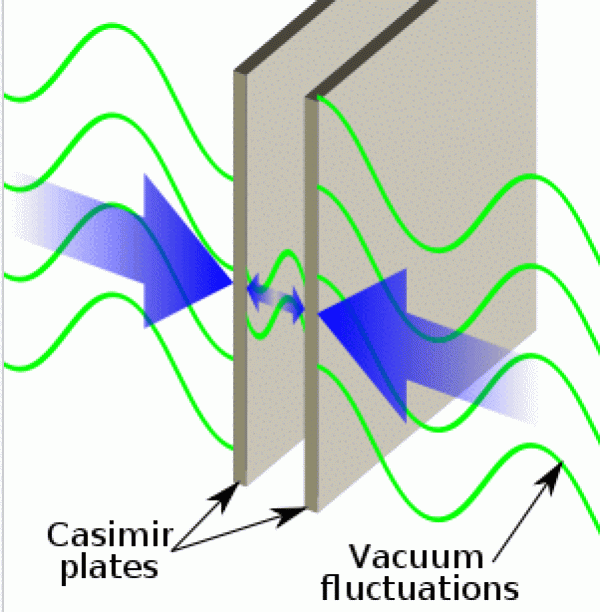Casimirův jev: Ve vakuu neustále vznikají a  zanikají virtuální částice a  silově působí na reálnou hmotu. Protože vznikají všude se stejnou hustotou a  narážejí na hmotu ze všech stran, jejich silové účinky se vyrovnají. Na částice lze pohlížet i  jako na vlny různých délek. Mezi dvěma blízkými rovnoběžnými deskami mohou vznikat pouze částice s  krátkou vlnovou délkou. Hustota částic je tu tedy menší a  tlak částic zvenčí převáží. Desky se k  sobě přitahují měřitelnou silou. Síla se zvětšuje se zmenšující se roztečí desek. S  jevem je třeba reálně počítat při návrhu mikrosoučástek. (Wikipedie)

Vraťme se k teleportu. Pokud nedokážeme principiálně zjistit polohu a hybnost částice, těžko se můžeme pokoušet na 3D tiskárně o její replikování (mimochodem, tytéž relace neurčitosti by nám to nedovolily, i kdybychom polohu a hybnost znali). Zdálo by se, že myšlenka teleportu je kvůli zákonům kvantové fyziky odsouzená živořit jen na stránkách fantastických románů. Přesto je to opět kvantová mechanika, která jisté řešení nabízí. Vychází z paradoxu, který zformulovali pánové Albert Einstein, Boris Podolsky a Nathan Rosen, když se pokoušeli zpochybnit jisté jevy pramenící z náhodnosti kvantové mechaniky. Naštěstí se ukázalo, že jsou tyto jevy sice paradoxní, ale správné. Nicméně článek Einsteina, Podolského a Rosena se stal klasikou a vstoupil do dějin pod názvem složeným z počátečních písmen jeho autorů: EPR paradox.

Jak by nám mohl pomoci při teleportaci? V podstatě jsou dvě možnosti. EPR nebo BEC. První možná zklame milovníky sci-fi, druhá snad potěší.

V minulém dílu jsme ukázali, že teleportace, tak jak si ji intuitivně představujeme, není možná. Brání v tom omezené možnosti poznat stav hmoty a tím pádem i nemožnost její replikace. Naznačili jsme, že východiskem by mohl být tzv. EPR paradox nazvaný podle počátečních písmen jmen Einsteina, Podolského a Rosena, kteří ho formulovali ve snaze zpochybnit nedeterminovanost kvantové mechaniky.

Ještě připomeňme, v čem nepoznatelnost systému spočívá. Jsou to Heisenbergovy relace neurčitosti, ze kterých mimo jiné plyne, že z principiálních důvodů můžeme současně zjistit polohu a hybnost částice pouze s omezenou přesností. Měříme-li polohu, ovlivňujeme hybnost a naopak při pokusu o změření hybnosti ovlivníme polohu.

Hybnost je definována jako součin hmotnosti a rychlosti. Pokud čtenář bude v tomto článku méně srozumitelný termín "hybnost" zatvrzele nahrazovat rychlostí, význam textu se příliš nezmění, jen je třeba mít stále na paměti, že ve skutečném světě by bylo zapotřebí uvažovat i hmotnosti jednotlivých částic.

Úvahami, které balancují na pomezí fyziky a filosofie, dospějeme k závěru, že dokud neprovedeme měření, pojmy hybnost a poloha ztrácejí význam, protože neexistují. Je to poněkud šokující tvrzení, z makrosvěta jsme zvyklí spíše na opačný přístup. Existují tu pojmy, které dávají smysl, jen do chvíle, než se jimi začneme zabývat hlouběji. Krásu Mony Lisy posuzujeme jen při pohledu z dálky. Ve chvíli, kdy ji chceme prozkoumat lupou, ztrácí pojem smysl a můžeme se bavit jen o barvě některých bodů na plátně, kterýžto pojem také přestane existovat, když se dostaneme na úroveň atomů.

Co se skrývá za pojmem EPR paradox: Zákony kvantové mechaniky nám sice neumožňují změřit dvě veličiny najednou, ale když se rozhodneme změřit pouze hybnost částice, není nic, co by nám zabránilo udělat to přesně. Pro jednoduchost předpokládejme, že je ta hybnost nulová (pokud by nebyla, byla by tu jen drobná výpočetní komplikace). Dejme tomu, že je částice radioaktivní a za nějakou dobu se rozpadne na dvě stejně hmotné komponenty A a B (většinou komponenty nejsou stejně hmotné, ale opět by to byla jen drobná výpočetní komplikace hmotnosti započítat), které se od sebe vzdalují. Po nějaké době změříme hybnost částice A a později třeba i polohu částice B. Protože měříme pokaždé pouze jednu vlastnost, můžeme tak učinit s libovolnou přesností. Dosud je vše v souladu s pravidly kvantové mechaniky i se zdravým rozumem. Pak ale přijde klasický fyzik a ukáže na spor. Jestliže známe hybnost částice A přesně, známe přesně i hybnost částice B. Je stejná, pouze má opačné znaménko, to přece plyne ze zákona zachování hybnosti. O částici B tak víme všechno. Polohu (tu jsme změřili) i hybnost (tu jsme dopočítali). A to je ve sporu s kvantovou mechanikou.

Zdravý rozum vidí řešení okamžitě. Relace neurčitosti neplatí, toto je důkaz. Ve skutečnosti je to pouze důkaz, že se zdravým rozumem v kvantové mechanice díru do světa neuděláme. Správné řešení je jinde. Od rozpadu až do okamžiku měření obě částice nevěděly o ničem jiném, než samy o sobě. Říkáme, že byly kvantově provázané neboli entanglované. Stále je mezi nimi jakési pouto, které zmizí ve chvíli interakce s nějakou další částicí, v našem případě ve chvíli měření hybnosti částice A. V ten okamžik se ztrácí i informace o hodnotě hybnosti částice B a v souladu s pravidly kvantové mechaniky nemáme šanci určit obě hodnoty přesně.

Einsteinovi se takové vysvětlení hrubě nelíbilo. Jeho teorie relativity je založená na předpokladu, že se informace nemůže šířit rychleji než světlo a zatím ji všechna měření potvrzují. V EPR paradoxu mohou být částice A a B od sebe světelné roky daleko, pak teprve provedeme měření na částici A a částice B pocítí změnu okamžitě.

Ve skutečnosti tu spor není. Opravdovou informaci tímto způsobem předat nemůžeme. Z toho, že na částici B nemůžeme provést dokonalé měření se nic nového nedozvíme. Teprve až nám někdo klasickou cestou zatelefonuje, jak dopadlo měření na částici A, můžeme potvrdit, že o B nevíme lautr nic.

V bulváru se občas objeví informace, že později Einstein nazval EPR paradox svou největší chybou života. Je to tak působivé rčení z úst fyzika takového kalibru, že se ho můžeme dočíst ve všech možných souvislostech, až nabudeme dojmu, že veškerá Einsteinova kariéra byla založena na jednom velkém nepochopení fyziky. Ve skutečnosti tuto větu použil pouze při sporu o rozpínání vesmíru. O EPR paradoxu nic takového neprohlásil a ani nemohl, protože spor byl definitivně rozhodnut až po jeho smrti.

Nyní máme již dostatek informací, abychom se mohli vrátit k původnímu tématu, k teleportaci. Chceme teleportovat částici C. Jinými slovy, chceme o ní zjistit dostatek informací k tomu, abychom ji mohli rekonstruovat na vzdáleném místě. Zatím jsme uvázli na tom, že nedokážeme zjistit o částici C všechny informace, brání nám v tom princip neurčitosti.

Z minulého pokusu máme připravený pár kvantově provázaných částic A a B. Zatím jsme na nich neprovedli měření, to je důležité, měřením se provázanost znehodnocuje. Necháme-li interagovat přenášenou částici C s částicí A, do částice B se přenesou všechny jinak nezjistitelné informace a ty ostatní musíme přenést klasickou cestou.

Proces je destruktivní, částice C je k nepoznání změněna, informace přenesená do částice B je z principu neuchovatelná, takže máme teleport, jak se patří. Na zdrojovém místě částice zmizí (nebo je alespoň k nepoužití), na cílovém je replikována a protože nemáme záznam, nemůžeme dělat kopie.

Dlouhou dobu byla teleportace technologicky nedosažitelným snem. Teprve v roce 1997 se podařilo teleportovat fotony ultrafialového světla a v roce 2004 dokonce celé atomy. Dodejme, že kvantové provázání částic se netýká pouze polohy a hybnosti, ale všech komplementárních veličin. S velkou oblibou (protože je to technicky nejméně náročné) je využíváno provázání částic pomocí spinu. Dvě částice, které spolu interagovaly, mají nulový výsledný spin. Jinými slovy, oba spiny jsou stejné až na znaménko.

Příznivce teleportu a la Star Trek teď asi zklamaně přeskakují zbytek článku. Vyřešili jsme problém, po kterém se ve sci-fi ani nevzdechne. Navíc je to způsob velice nepraktický. Na transport pana Spocka by bylo třeba předem dopravit na zdrojové a cílové místo celé kilogramy provázaných částic, které již nesmí interagovat ani mezi sebou a do chvíle přenosu ani s okolím. Omezení, že částice C musí být stejného typu jako A a B, je z tohoto pohledu jen zanedbatelná komplikace.

A přece to není vše! Na transport pana Spocka si stále ještě netroufneme, ale jak se vyhnout problematickému generování a udržování provázaných párů částic už víme. V roce 2007 byl navržen mechanismus teleportace pomocí Bose-Einsteinova kondensátu, zkráceně BEC.

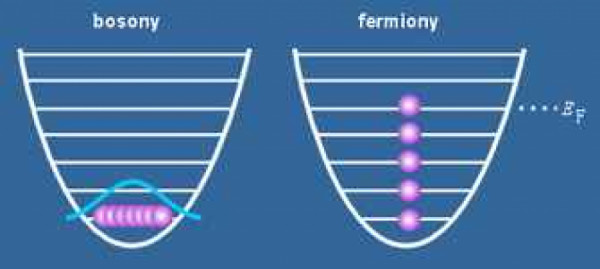Bosony s oblibou zaujímají stejný energetický stav. Naproti tomu fermiony díky své nesnášenlivosti upřednostňují volné energetické hladiny. (Aldebaran)

K vysvětlení pojmu BEC je nejprve třeba ozřejmit, že částice můžeme rozdělit do dvou skupin. Hrubě řečeno, jedny tvoří hmotu, na kterou si můžeme sáhnout (protony, neutrony, elektrony...), ty druhé jsou nehmatatelné, třeba fotony. První typ částic nazýváme fermiony a mají jednu pozoruhodnou vlastnost. Vzpírají se tomu, aby zaujaly stejný stav. Právě fermionům vděčíme za rozmanitost přírody. Je to jejich nesnášenlivost, díky které jsou schopny tvořit rozmanité struktury. Kdyby atomy tuto vlastnost neměly, vesmír by byl jen prostorem, kterým poletují elementární částice neschopné vytvořit ani atom. Právě takové vlastnosti mají bosony.

Matematicky se dají rozlišit velice snadno, podle vlastnosti, která se nazývá spin. V tuto chvíli není důležité vědět, co to spin je, stačí ho pokládat za číselný rozpoznávač bosonů a fermionů. Bosony mají spin celočíselný, fermiony neceločíselný v násobcích jedné poloviny. Proč právě takhle? Je to víceméně z historických důvodů. Kdyby bylo nejprve zvládnuto statistické chování fermionů, nejspíše bychom dnes říkali, že mají spin lichý, zatím co bosony sudý. Vývoj šel jinak, proto máme poloviční spiny.

O jedné kouzelné vlastnosti spinů jsme se ještě nezmínili. Dají se za určitých okolností sčítat. Ty okolnosti se naplno rozvíjejí za velice nízkých teplot, typicky při zlomcích milikelvinů. Tehdy zaujmou všechny fermiony nejnižší energetické stavy. Jaký je výsledný spin atomu se sudým počtem fermionů? Samozřejmě, že celočíselný. Atom se pak chová jako boson a je ochoten s ostatními atomy zaujmout stejné místo. Tomuto stavu říkáme Bose-Einsteinův kondenzát. Poprvé byl připraven v roce 1995 na přibližně dvou tisících atomech rubidia. Všechny tyto atomy obsadily na celých 15 s jedno místo a chovaly se jako jediný superatom.

Zařízení na výrobu Bose-Einsteinova kondenzátu. (Aldebaran)

Nápadů, co všechno by se s BEC dalo podniknout, je více než laboratoří, které jsou zatím schopny BEC připravit. Mluví se o atomových laserech, využití v kvantových počítačích... Nás teď zajímá teleportace. Ta by probíhala následovně: Na atomy hmoty, kterou chceme teleportovat, necháme působit BEC připravené z atomů stejného prvku. Teleportované atomy při setkání s BEC budou chtít zaujmout stejně nízké energetické stavy a přebytečnou energii vyzáří ve formě světelného záblesku. V tomto záblesku jsou obsaženy všechny informace o původní teleportované hmotě. V cíli necháme paprsek narazit do dalšího BEC, který jeho veškerou energii pohltí a nechá atomy zaujmout jejich původní polohy.

Takový způsob teleportace vypadá velice nadějně. Ačkoli je jasné, že k přenesení makroskopických předmětů na dálku je ještě potřeba ujít dlouhou cestu, na které se mohou objevit zásadní nepřekonatelné překážky, nemusíme při teleportaci pana Spocka protáčet panenky. V desátém dílu sci-fi povídky Benzínka na Japetu se můžete dočíst, k čemu může dojít, když je teleportace kombinována se změnou gravitačního potenciálu.

Errata: