Vítej, návštěvníku!

Newtonovy zákony jsou snadné na pochopení. Odráží jen naši každodenní zkušenost. Opravdu jim ale rozumíme?

Ve sci-fi povídce Na dohled Cruithne (kapitola 12) zachrání kosmonaut v otevřeném vesmíru druhého kosmonauta tím, že ho odkopne směrem k lodi. Sám se tím obětuje, protože odlétá na druhou stranu přesně podle zákona akce a reakce. Je to jeden ze tří Newtonových zákonů. Ačkoli si myslíme, že jsou to bezproblémové zákony, u každého ukážeme, že tomu tak není. Aby bylo jasno, Newtonovy zákony nemají problém s popisem reality, problém nastává, když si lidé neuvědomují, že by se na ně měli odvolávat.

Těleso setrvává v klidu nebo rovnoměrném přímočarém pohybu, není-li nuceno vnějšími silami tento stav změnit.

Zákon je jasný. Opravdu se nestává, že by se cihla dala sama od sebe do pohybu, nebo aby naopak auto okamžitě zastavilo, když sundáme nohu z plynu. A teď si poslechněme, jak žák vysvětluje, proč nespadne Měsíc z nebe.

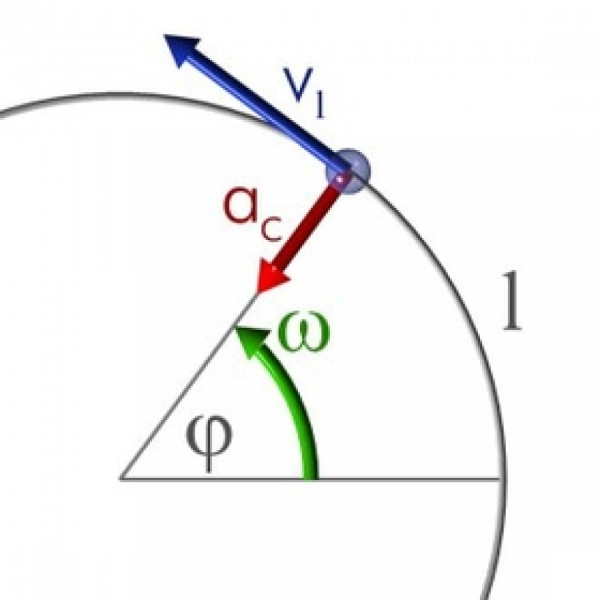Těleso pohybující se po kružnici rychlostí -v- a dostředivé zrychlení -a-. (Wikipedie)

Jak Měsíc obíhá kolem Země, působí na něj odstředivá síla, která se vyruší s přitažlivou silou Země. Takže na něj nepůsobí žádná síla a nemá, proč by spadl.

Pan učitel spokojeně pokyvuje a jedničkou do žákovské stvrzuje neplatnost prvního Newtonova zákona. Jestliže na Měsíc nepůsobí žádná síla, měl by přece podle tohoto zákona stát na místě, nebo odletět po přímce pryč.

Nežehrejme kvůli tomu na pana učitele ani jeho žáka. V podstatě si uvědomují, v čem je jádro problému, jen to špatně vyjadřují. Na vině je samotný pojem odstředivé síly. Jakkoli je tento pojem užitečný v běžné mluvě, při hlubším ponoření do problému se stává poněkud komplikovaným. Spíš bychom měli mluvit o reakci na sílu dostředivou, v tomto případě na gravitaci. Tím se dostáváme k dalšímu zákonu, k zákonu akce a reakce.

Proti každé akci vždy působí stejná reakce

Ani s tímto zákonem nemáme problém. Při výstřelu kulky z pušky (akce) nás do ramene praští pažba (reakce). Zákon se dá rozepsat i kvantitativně, takže můžeme dopočítat, jak moc puška ucukne. Pro naše účely to ani potřebovat nebudeme.

Magdeburské polokoule. Ani čtyři páry koní na každé straně nedokázaly rozdělit evakuovanou nádobu. (iDnes)

Vraťme se teď o nějakých 350 let zpět, do doby pokusu na obrázku. Německý fyzik Otto von Guericke demonstroval jistý pokus spojený s tlakem vzduchu. Podstata pokusu pro nás není důležitá. Zajímá nás, proč při pokusu odtrhnout od sebe dvě přisáté polokoule zapřáhl na každou stranu osm koní.

Odpověď je jasná. Je to podvod na přihlížející. Osm koní na každé straně dělá dojem, že ani síla, kterou dokáže vyvinout šestnáct koní, nedokáže polokoule roztrhnout. Taková síla tam ale nikde nefiguruje.

Vraťme se zpět k panu Newtonovi a podívejme se na zákon akce a reakce z druhé strany. Osm koní táhne nalevo, osm napravo. Protože je vše v klidu, polokoule se nevychyluje na žádnou stranu, můžeme mluvit o akci a reakci. Vidíme, že se dřou obě skupiny koní, ale přitom ta jedna je jen reakcí na působení té druhé. Síla, kterou vyvinou, neodpovídá dvěma spřežením, ale jen jednomu.

Kdyby pan Guericke jednu stranu přivázal ke stoletému dubu, jedno spřežení by ušetřil a silový účinek by byl tentýž. Kdyby nyní ušetřené spřežení připřáhl k prvnímu, tak aby všichni koně táhli stejným směrem, možná by polokoule od sebe odtrhl. Síla by odpovídala tahu šestnácti koní. A stoletý dub? Ten by dělal této síle reakci, takže by táhl stejnou silou, jen opačným směrem.

Rozvedeme-li zákon akce a reakce kousek dál, dostaneme se k deformačním účinkům a bude nám zřejmé, kde udělal chybu v úvaze jistý obhájce neomezené rychlosti v obci.

Je to již poměrně dávno, tenkrát se v obci smělo jezdit 60km/h. Je to údajně i maximální rychlost, při které ještě dokáže bezpečnostní pás ochránit jezdce na předním sedadle. Úvaha zněla následovně. Limit 60km/h nemá smysl, protože při čelní srážce mají automobily beztak vzájemnou rychlost 120km/h.

Ponechme stranou ostatní logické kotrmelce a věnujme se fyzice. Vzájemná rychlost bude skutečně 120km/h, ale to neznamená, že by deformační účinky byly stejné, jako kdyby řidič při této rychlosti naboural do betonové zdi. Automobil kolidující z protisměru vytváří jen reakci. Oba automobily ve chvíli srážky zbrzdí z rychlosti 60km/h na nulu. Pokud platí výše uvedený teorém o bezpečnostních pásech, zůstává slušná šance, že se nepřetrhnou.

Tato úvaha platí samozřejmě při srážce dvou stejných vozů. V reálu by měl navrch ten těžší.

Jestliže na těleso působí síla, pak se těleso pohybuje se zrychlením, které je přímo úměrné působící síle a nepřímo úměrné hmotnosti tělesa.

Třetí Newtonův zákon je známější asi ve své kvantitativní podobě jako vzorec

F = m a

Při interpretaci většinou nečiní výraznější potíže, příklady vycházívají, žákům jak mají. Problém je spíše v rovině filosofické. Vztah vypadá jako definice síly. Bohužel není to pravda. Newtonovská fyzika je sice na síle založená, ale definice pojmu chybí. Ukážeme si to právě na tomto případě.

Síla je definována pomocí zrychlení. Pak je samozřejmě legitimní ptát se, co je to zrychlení. Odpověď je jednoduchá. Je to změna rychlosti s časem. Lapidárně řečeno, hodnota zrychlení nám říká, jak rychle se mění rychlost tělesa. Třeba jak dlouho trvá automobilu, než zrychlí z devadesáti na stovku. Vyjádříme to vztahem

a = v / t

A co je to rychlost? To už zná snad každý. To jsou ty kilometry za hodinu, co máme na tachometru, neboli změna dráhy za čas.

A dráha? To je rozdíl souřadnic dvou bodů. Že je to definice krkolomná a že dokáži změřit vzdálenost i bez souřadné soustavy, třeba pásmem? Nevěřte tomu, i při měření pásmem zakládám nevědomky nějakou svou souřadnou soustavu s počátkem ve výchozím bodě a osou definovanou přikládaným měřítkem.

Výpočet dráhy mám tedy definovaný, jen je třeba se ještě zeptat na to, jaká souřadná soustava to má být. Libovolná, třeba spojená s kolotočem? To jistě ne, víme, že na kolotoči by se do měření pletla spousta dalších faktorů. Když to promyslíme hlouběji, budeme požadovat tak zvanou setrvačnou neboli inerciální vztažnou soustavu.

Výborně. A co je to inerciální vztažná soustava? To je vztažná soustava, ve které platí Newtonovy zákony. Jinými slovy, soustava, ve které na těleso nepůsobí žádné síly. Žádné síly? A co je to síla? Naše definice se uzavřela v bludném kruhu.

Obecná relativita a kvantová teorie

Absence definice síly je vážná koncepční trhlina v newtonovské mechanice. Můžeme tedy jen s úctou nahlížet, jak mocná tato teorie je. Díky ní se nám daří popsat naprostou většinu jevů, se kterými se denně setkáváme, od popisu miniaturních hodinek, přes kosmické rakety až po pohyb hvězd v naší Galaxii. Začíná selhávat teprve při velkých rychlostech, obrovských hmotách nebo na druhou stranu v mikrosvětě, při popisu světa atomů. Kvantová teorie ani obecná relativita tento problém nemají, protože pojem síly vůbec nezavádějí.

Selhávání newtonovského přístupu se přitom děje leckdy zvláštním způsobem. Čekali bychom, že v okrajových hodnotách budou výsledky klasické mechaniky stále méně a méně přesné. A tak tomu skutečně velice často je. Jsou ale případy, kdy nás výsledky nutí k zamyšlení.

Pomocí klasické mechaniky rozšířené o představu, že světlo je proud rychle letících hmotných kuliček, lze například předpovědět existenci černé díry. Co víc, po dosazení do vzorce pro druhou kosmickou rychlost získáme i vztah pro výpočet poloměru černé díry, který je stejný, jaký dává obecná teorie relativity. Problém je v tom, že oba vzorce, ač stejné, vyjadřují pokaždé něco jiného. Obecná relativita tvrdí, že ani světlo nedokáže překonat gravitační propast. Z klasického přístupu plyne, že by se světlo ven dostat mohlo, ale stále by zpomalovalo a v nekonečné vzdálenosti by se zastavilo. To je samozřejmě pošetilá představa, ale dává číselně stejný výsledek.

Podobné zvláštnosti můžeme najít třeba i v popisu ohybu světla v gravitačním poli nebo naopak při pokusu o odvození některých aspektů mikrosvěta. Dá se sice matematicky ukázat, že to tak být musí, protože příslušné výpočty se tak chovají. Po světonázorové stránce se s tím však musí vypořádat každý dle své nátury.

Errata:

30.05.2021 13:06